引言:本文主要是对当前细化代码以及原理做一个分析总结,持续更新ing
前言
细化是将图像的线条从多像素宽度减少到单位像素宽度过程的简称,一些文章经常将细化结果描述为”骨架化”。
一般要求:
- 1、保证细化后骨架的连通性;
- 2、对原图像的细节特征要保持的较好;
- 3、细化的结果是原线条的中心线;
- 4、线条的端点保留完好;
- 5、线条交叉点不能发生畸变;
- 6、细化所用时间不能太长。
算法
非迭代算法
非迭代细化算法是不以像素为基础的,它们通过一次遍历的方式产生线条的某一中值或中心线,而不检查所有单个像素,即这种算法是一次即产生骨架;如基于距离变换的方法,游程长度编码细化等。这类算法中最简单的方法是通过扫描确定每段线的中心点,然后把它们连接成一副骨架,这种算法拥有计算机处理速度的优势,但是会有容易产生噪声点的缺陷。
迭代算法
即重复删除图像边缘满足一定条件的像素,最终得到单像素宽带骨架。 迭代方法依据其检查像素的方法又可以再分成:
串行算法: 在串行算法中,通过在每次迭代中用固定的次序检查像素来判断是否删除像素,在第n次迭代中像素p的删除取决于到目前为止执行过的所有操作,也就是必须在第(n-1)次迭代结果和第n次检测像素的基础之上进行像素删除操作;即是否删除像素在每次迭代的执行中是固定顺序的,它不仅取决于前次迭代的结果,也取决于本次迭代中已处理过像素点分布情况。
并行算法: 在并行算法中,第n次迭代中像素的删除只取决于(n-1)次迭代后留下的结果,因此所有像素能在每次迭代中以并行的方式独立的被检测;即像素点删除与否与像素值图像中的顺序无关,仅取决于前次迭代效果
1、基于数学形态学的细化算法
数学形态学细化算法的主要思想是源于击中击不中变换的形态学算法。在给定一系列具有一定形状的结构元素后,顺序循环地删除满足击中变换的像素。 细化公式:\(A\otimes B=A-\left ( A\otimes B \right )\)
2、Zhang快速并行算法
Zhang快速并行算法是Zhang在1984年提出来的。以二值图像为例,判断一个点该不该删除时要根据它的八个相邻点的情况来判断。总结一下,有如下的判据:
- 1、内部点不能删除
- 2、孤立点不能删除
- 3、直线端点不能删除
- 4、如果P是边界点,去掉P后,如果连通分量不增加,则P可以删除。
该算法步骤如下:假设一幅图像中的3*3区域,对各点标记名称P1、P2、…、P9,其中P1位于中心,如下图
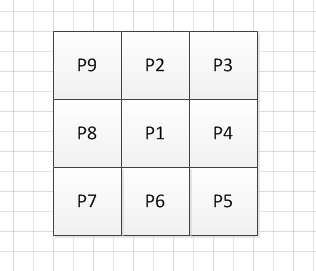
算法步骤
1、其中P1=1为黑色点,如果同时满足以下四个条件,则删除P1,即令P1=0
- 1、P1周围的8个点中,白点的个数介于2至6,则 2≤N(P1)≤6;其中,N(P1)=P2+P3+…+P9;这一步是为了排除孤立点和内部点。
- 2、设Z(P1)是以P2、…、P9为序时这些点的值从0到1变化的次数,也就是表示从P2按顺序到P9的过程中,相应的点的数值从0->1的变化次数。当对所有边界点都检查完毕后,将所有标记了的点除去。
- 3、P2×P4×P6=0;
- 4、P4×P6×P8=0;
2、同1,仅将上面3条件改为P2×P4×P8=0;4条件改为P2×P6×P8=0。同样当对所有边界点都检验完毕后,将所有标记了的点除去。
3、以上两步操作构成一次迭代,直至没有点再满足标记条件,这时剩下的点组成区域即为细化后的骨架。
代码
void thinimage(Mat &srcimage)//单通道、二值化后的图像
{
vector<Point> deletelist1;
int Zhangmude[9];
int nl = srcimage.rows;
int nc = srcimage.cols;
while (true)
{
for (int j = 1; j<(nl - 1); j++)
{
uchar* data_last = srcimage.ptr<uchar>(j - 1);
uchar* data = srcimage.ptr<uchar>(j);
uchar* data_next = srcimage.ptr<uchar>(j + 1);
for (int i = 1; i<(nc - 1); i++)
{
if (data[i] == 255)
{
Zhangmude[0] = 1;
if (data_last[i] == 255) Zhangmude[1] = 1;
else Zhangmude[1] = 0;
if (data_last[i + 1] == 255) Zhangmude[2] = 1;
else Zhangmude[2] = 0;
if (data[i + 1] == 255) Zhangmude[3] = 1;
else Zhangmude[3] = 0;
if (data_next[i + 1] == 255) Zhangmude[4] = 1;
else Zhangmude[4] = 0;
if (data_next[i] == 255) Zhangmude[5] = 1;
else Zhangmude[5] = 0;
if (data_next[i - 1] == 255) Zhangmude[6] = 1;
else Zhangmude[6] = 0;
if (data[i - 1] == 255) Zhangmude[7] = 1;
else Zhangmude[7] = 0;
if (data_last[i - 1] == 255) Zhangmude[8] = 1;
else Zhangmude[8] = 0;
int whitepointtotal = 0;
for (int k = 1; k < 9; k++)
{
whitepointtotal = whitepointtotal + Zhangmude[k];
}
if ((whitepointtotal >= 2) && (whitepointtotal <= 6))
{
int ap = 0;
if ((Zhangmude[1] == 0) && (Zhangmude[2] == 1)) ap++;
if ((Zhangmude[2] == 0) && (Zhangmude[3] == 1)) ap++;
if ((Zhangmude[3] == 0) && (Zhangmude[4] == 1)) ap++;
if ((Zhangmude[4] == 0) && (Zhangmude[5] == 1)) ap++;
if ((Zhangmude[5] == 0) && (Zhangmude[6] == 1)) ap++;
if ((Zhangmude[6] == 0) && (Zhangmude[7] == 1)) ap++;
if ((Zhangmude[7] == 0) && (Zhangmude[8] == 1)) ap++;
if ((Zhangmude[8] == 0) && (Zhangmude[1] == 1)) ap++;
if (ap == 1)
{
if ((Zhangmude[1] * Zhangmude[7] * Zhangmude[5] == 0) && (Zhangmude[3] * Zhangmude[5] * Zhangmude[7] == 0))
{
deletelist1.push_back(Point(i, j));
}
}
}
}
}
}
if (deletelist1.size() == 0) break;
for (size_t i = 0; i < deletelist1.size(); i++)
{
Point tem;
tem = deletelist1[i];
uchar* data = srcimage.ptr<uchar>(tem.y);
data[tem.x] = 0;
}
deletelist1.clear();
for (int j = 1; j<(nl - 1); j++)
{
uchar* data_last = srcimage.ptr<uchar>(j - 1);
uchar* data = srcimage.ptr<uchar>(j);
uchar* data_next = srcimage.ptr<uchar>(j + 1);
for (int i = 1; i<(nc - 1); i++)
{
if (data[i] == 255)
{
Zhangmude[0] = 1;
if (data_last[i] == 255) Zhangmude[1] = 1;
else Zhangmude[1] = 0;
if (data_last[i + 1] == 255) Zhangmude[2] = 1;
else Zhangmude[2] = 0;
if (data[i + 1] == 255) Zhangmude[3] = 1;
else Zhangmude[3] = 0;
if (data_next[i + 1] == 255) Zhangmude[4] = 1;
else Zhangmude[4] = 0;
if (data_next[i] == 255) Zhangmude[5] = 1;
else Zhangmude[5] = 0;
if (data_next[i - 1] == 255) Zhangmude[6] = 1;
else Zhangmude[6] = 0;
if (data[i - 1] == 255) Zhangmude[7] = 1;
else Zhangmude[7] = 0;
if (data_last[i - 1] == 255) Zhangmude[8] = 1;
else Zhangmude[8] = 0;
int whitepointtotal = 0;
for (int k = 1; k < 9; k++)
{
whitepointtotal = whitepointtotal + Zhangmude[k];
}
if ((whitepointtotal >= 2) && (whitepointtotal <= 6))
{
int ap = 0;
if ((Zhangmude[1] == 0) && (Zhangmude[2] == 1)) ap++;
if ((Zhangmude[2] == 0) && (Zhangmude[3] == 1)) ap++;
if ((Zhangmude[3] == 0) && (Zhangmude[4] == 1)) ap++;
if ((Zhangmude[4] == 0) && (Zhangmude[5] == 1)) ap++;
if ((Zhangmude[5] == 0) && (Zhangmude[6] == 1)) ap++;
if ((Zhangmude[6] == 0) && (Zhangmude[7] == 1)) ap++;
if ((Zhangmude[7] == 0) && (Zhangmude[8] == 1)) ap++;
if ((Zhangmude[8] == 0) && (Zhangmude[1] == 1)) ap++;
if (ap == 1)
{
if ((Zhangmude[1] * Zhangmude[3] * Zhangmude[5] == 0) && (Zhangmude[3] * Zhangmude[1] * Zhangmude[7] == 0))
{
deletelist1.push_back(Point(i, j));
}
}
}
}
}
}
if (deletelist1.size() == 0) break;
for (size_t i = 0; i < deletelist1.size(); i++)
{
Point tem;
tem = deletelist1[i];
uchar* data = srcimage.ptr<uchar>(tem.y);
data[tem.x] = 0;
}
deletelist1.clear();
}
}
3、Hilditch算法
Hilditch细化算法为是串行处理方法的一种,是一种经典的,充分利用连接数的算法。其主要原理是每次扫描并删除图像上满足一定的条件的轮廓像素,直到图像上不存在可删除的轮廓像素为止。该方法适用于二值图像,即像素为1的区域为目标区域,像素为0的区域为背景区域的图像。在此算法中,目标像素P若同时满足以下条件即为可删除像素:
- 1、p的灰度值为1,即p是前景点,不是背景;
- 2、P0+P2+P4+P6≤3,(则三个不全为1,否则删除P,会造成图像空心)
- 3&4、Pk(0≤k≤7)中至少有两个目标像素为1(若只有一个255,则P是图像的某个端点,不能删除否则影响图像性质;若没有255,则p是孤立点,也不能删除) (代码中的条件 3&4)
- 5、连通性检测,Nc=1
- 6、宽度为2的骨架只能删除一边
#define GRAY 128
#define WHITE 255
#define BLACK 0
int func_nc8(int *b)
//端点的连通性检测
{
int n_odd[4] = { 1, 3, 5, 7 }; //四邻域
int i, j, sum, d[10];
for (i = 0; i <= 9; i++) {
j = i;
if (i == 9) j = 1;
if (abs(*(b + j)) == 1)
{
d[i] = 1;
}
else
{
d[i] = 0;
}
}
sum = 0;
for (i = 0; i < 4; i++)
{
j = n_odd[i];
sum = sum + d[j] - d[j] * d[j + 1] * d[j + 2];
}
return (sum);
}
void cvHilditchThin(cv::Mat& src, cv::Mat& dst)
{
if(src.type()!=CV_8UC1)
{
printf("只能处理二值或灰度图像\n");
return;
}
//非原地操作时候,copy src到dst
if(dst.data!=src.data)
{
src.copyTo(dst);
}
//8邻域的偏移量
int offset[9][2] = {{0,0},{1,0},{1,-1},{0,-1},{-1,-1},{-1,0},{-1,1},{0,1},{1,1} };
//四邻域的偏移量
int n_odd[4] = { 1, 3, 5, 7 };
int px, py;
int b[9]; //3*3格子的灰度信息
int condition[6]; //1-6个条件是否满足
int counter; //移去像素的数量
int i, x, y, copy, sum;
uchar* img;
int width, height;
width = dst.cols;
height = dst.rows;
img = dst.data;
int step = dst.step ;
do
{
counter = 0;
for (y = 0; y < height; y++)
{
for (x = 0; x < width; x++)
{
//前面标记为删除的像素,我们置其相应邻域值为-1
for (i = 0; i < 9; i++)
{
b[i] = 0;
px = x + offset[i][0];
py = y + offset[i][1];
if (px >= 0 && px < width && py >= 0 && py <height)
{
// printf("%d\n", img[py*step+px]);
if (img[py*step+px] == WHITE)
{
b[i] = 1;
}
else if (img[py*step+px] == GRAY)
{
b[i] = -1;
}
}
}
for (i = 0; i < 6; i++)
{
condition[i] = 0;
}
//条件1,是前景点
if (b[0] == 1) condition[0] = 1;
//条件2,是边界点
sum = 0;
for (i = 0; i < 4; i++)
{
sum = sum + 1 - abs(b[n_odd[i]]);
}
if (sum >= 1) condition[1] = 1;
//条件3, 端点不能删除
sum = 0;
for (i = 1; i <= 8; i++)
{
sum = sum + abs(b[i]);
}
if (sum >= 2) condition[2] = 1;
//条件4, 孤立点不能删除
sum = 0;
for (i = 1; i <= 8; i++)
{
if (b[i] == 1) sum++;
}
if (sum >= 1) condition[3] = 1;
//条件5, 连通性检测
if (func_nc8(b) == 1) condition[4] = 1;
//条件6,宽度为2的骨架只能删除1边
sum = 0;
for (i = 1; i <= 8; i++)
{
if (b[i] != -1)
{
sum++;
} else
{
copy = b[i];
b[i] = 0;
if (func_nc8(b) == 1) sum++;
b[i] = copy;
}
}
if (sum == 8) condition[5] = 1;
if (condition[0] && condition[1] && condition[2] &&condition[3] && condition[4] && condition[5])
{
img[y*step+x] = GRAY; //可以删除,置位GRAY,GRAY是删除标记,但该信息对后面像素的判断有用
counter++;
//printf("----------------------------------------------\n");
//PrintMat(dst);
}
}
}
if (counter != 0)
{
for (y = 0; y < height; y++)
{
for (x = 0; x < width; x++)
{
if (img[y*step+x] == GRAY)
img[y*step+x] = BLACK;
}
}
}
}while (counter != 0);
}